Leyendo el periódico me he topado con una noticia un tanto luctuosa: Tres de cada cinco niños muertos en accidente viajaban sin cinturón. Por tema y por formato se parece mucho a otras, demasiadas, que hemos ido escuchando en los últimos tiempos, como en las últimas vacaciones de semana santa: El 48% de los muertos en accidente de tráfico en Semana Santa no llevaba el cinturón de seguridad.
Pero aunque os pido encarecidamente que toméis todas las precauciones posibles cuando salgáis a la carretera, no quería hablaros del tema de la seguridad al volante. Sólo necesito que os quedéis con la "morfología" de estas noticias, o la estructura lógica de la información que nos están dando (no sé cómo expresarlo, perdonadme). Porque tiene mucho que ver con ese tema tan específico y tan elevado en su torre de marfil que es el aprendizaje de relaciones de causalidad. Así que por favor no os fijeis ahora en el contenido de las noticias, ciertamente desagradable, y quedaos con la forma, que es lo que me interesa en este momento. Vamos al ajo:
"El 48% de los muertos al volante no llevaba el cinturón". Esa es la información que nos dan en una noticia en concreto. ¿Qué conclusiones podemos sacar? Según mi interpretación, más bien pocas y poco informativas. Podemos contemplar la situación como el cruce de dos variables, discretas y dicotómicas: Primero, el hecho de llevar o no el cinturón de seguridad, y por otro lado, el resultado de muerte en accidente (presente o ausente, porque no se admiten grados en eso de pasar al descanso eterno, ¿verdad?). Con el cruce de las dos variables obtenemos una matriz 2x2 (con cuatro celdas) que contiene todas las situaciones posibles:

Esto es una tabla similar a las que solemos emplear en el estudio del aprendizaje de causalidad. Una tabla de contingencia, en la que podemos representar la información de que disponemos acerca de la realidad. Vale, sabemos que el 48% de los muertos no llevaba el cinturón, según la noticia. Entonces la frecuencia de los eventos tipo c es 0,24 (0,48 dividido entre 2, porque la suma de las cuatro celdas nos debe dar el total de 100%). Eso significa, naturalmente, que la frecuencia de los eventos tipo a es 0,52 entre 2 (0,26). Ya es llamativo que haya más muertos que lleven el cinturón que sin él, pero pasémoslo por alto.
Lo verdaderamente curioso es que, como podemos observar, la información que nos proporciona la estadística del periódico es prácticamente inútil, por incompleta. No puedo saber hasta qué punto es importante el uso del cinturón sin que me ofrezcan ningún dato sobre las celdas b y d, las que me dicen qué pasa con los conductores que no mueren en los accidentes: ¿llevan el cinturón esos supervivientes o no? Esas dos celdas constituyen lo que llamamos la tasa base, y claramente son necesarias para saber si el cinturón ha sido efectivo.
Imaginemos la siguiente noticia, por exagerar las cosas: "El 80% de los conductores muertos en accidente no llevaban el cinturón". De nuevo es una información incompleta que sólo nos habla de a y c. Y aparentemente, es un buen argumento para abrocharse el cinturón. Pero, ¿Y si nos dan la información que falta y así descubrimos también que la celda d tiene la misma frecuencia que la celda c? O sea, hablando en cristiano, ¡que el 80% de los que no mueren en el accidente también llevan el cinturón desabrochado! Algo así:

Significaría que la probabilidad de morir es la misma con el cinturón abrochado que desabrochado. Que el cinto no serviría para nada. Precisamente lo contrario de lo que pretende decir la noticia, ¿verdad? La única conclusión que podemos sacar de esta matriz es que casi todos los conductores accidentados (el 80%) pasan de usar el cinturón, y que la mitad de ellos muere y la otra mitad no.
También podría ocurrir, con esa misma redacción de la noticia, que la información que no nos han contado tuviese un contenido muy distinto (como no nos lo cuentan, somos libres de imaginar lo que queramos):
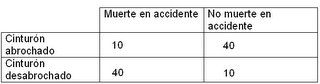
Efectivamente, según esta otra distribución, que concentra la mayoría de los casos en las celdas b y c, el cinturón es muy efectivo a la hora de prevenir la muerte en un accidente. De hecho, para ser informativa, la noticia debería añadir "... y el 80% de los que no mueren lo lleva abrochado".
De nuevo reitero mis disculpas por no haber buscado un ejemplo un poco más agradable. Al fin y al cabo, todos tenemos algún conocido que ha sufrido un accidente de tráfico (no me extraña, con estas cifras que se manejan es pura verdad estadística que le toque a uno). Pero no os quedéis sólo en el contenido, pensad en la forma de la información que nos llega. Los redactores pretenden con sus noticias convencer a los conductores de la necesidad de ser prudentes y de utilizar mecanismos de seguridad pasivos. Pero sucede que, precisamente por no darnos toda la información necesaria para establecer un buen juicio de causalidad, no llegan a ser lo efectivos que deberían en la comunicación de los datos. O eso me ha parecido hace un momento al leer el periódico.
Por favor, tened mucho cuidado si cogéis el coche estos días. No bebáis, no corráis, no olvidéis poneros el cinturón ni tengáis prisa por llegar. Y buen viaje. A mí aún me quedan unos cuantos días para marchar :-)









7 comentarios:
Excelente apunte, Gilgamesh. Creo que el problema de los redactores de noticias tiene que ver con la dificultad para cuantificar de manera precisa y fidedigna las frecuencias de las celdas b y d.
Por un lado, es más complicado hacer recuento de uso de cinturón de seguridad en caso de accidente no mortal porque hay una mayor cantidad de accidentes no mortales y quizá muchos pasen desapercibidos (si no tienes un seguro, no te conviene llamar a la policía). Por otro lado, en caso de accidente no mortal uno debería basarse en la información provista por el conductor y/o sus acompañantes. Vamos, que si sales por tu propio pie de un accidente y te preguntan si llevabas el cinturón puesto, puedes decir "sí" o "no" con absoluta libertad, sin que tu respuesta sea necesariamente cierta. Por supuesto, dirás que sí para evitar una multa... ¿verdad? Por tanto, los que hacen esas estadísticas no pueden tomar como fiable la información que les llega sobre las celdas b y d.
la conclusión es clara, si de los que llevaban el cinturón puesto alcanzan el 52 %, quiere decir que es peor llevarlo que no llevarlo puesto
Kaiho: me temo que eso no es del todo correcto. Verás, el problema de esa noticia es que sólo nos dice qué ha pasado con los accidentados que han muerto: "el 48% de los muertos en accidente no llevaba puesto el cinturón". De esa información, lo único que podemos concluir es que el 52% de los muertos sí lo llevaba puesto, pero nada más. Lo realmente importante para saber si el cinturón funciona o no funciona es saber qué es lo que pasa con los accidentados que han sobrevivido: los que sobrevivieron, ¿llevaban el cinto? ¿en qué porcentaje?
Como no nos dan esa información, somos libres de imaginar cualquier escenario posible. Para ilustrarte el asunto, te pongo los ejemplos extremos:
-Imagina que nos dan esas mismas cifras: de los muertos, el 48% sin cinturón, el 52% con él. Y averiguamos que, entre los supervivientes, el 90% lleva cinturón y el 10% no.
Eso significa que si llevas el cinturón es más probable sobrevivir. ¿No lo ves claro?
-Con las mismas cifras para los muertos, imagina que con los vivos te damos otros números: el 10% lleva cinturón, el 90% no. Eso significa que el cinturón no sólo no salva vidas sino que es peligroso. Es más probable sobrevivir si no llevas el cinturón.
-También podría darse una última posibilidad: que las cifras fuesen las mismas entre los vivos y entre los muertos: 48% no llevan cinturón, 52% sí lo llevan. Eso significa sencillamente que el cinturón no funciona en absoluto. La probabilidad de vivir o morir es la misma llevándolo puesto que no llevándolo.
¿Que cómo llego a estas conclusiones sobre la efectividad del cinturón a partir de la información de los supervivientes? Sí, lo sé, parece un salto un poco brusco, pero ahora te lo explico, auqnue te aviso que el camino va a ser un poco largo:
Cuando hablamos de causalidad, es decir, de si un determinado evento produce a otro (en este caso, llevar el cinturón produce la supervivencia), realmente estamos basándonos en un concepto llamado "contingencia", que no es más que la medida de la covariación entre dos o más variables discretas y dicotómicas (alaaaa, cuanto palabro seguido, no te preocupes: cuando digo discretas, sólo me refiero a que no toman valores infinitos, y cuando digo dicotómicas sólo me refiero a que pueden tomar dos valores, sí/no, presente/ausente, encendido/apagado...). Simplificando, si un evento A se da siempre que se presenta otro evento B, y nunca en otro momento, podemos decir que la contingencia A-B es positiva y alta. La contingencia negativa indicaría la relación contraria: A siempre aparecería en ausencia de B y sólo en su ausencia. Y la contingencia cero o nula representaría la aleatoridad: A aparecerían a veces en presencia de B, a veces en su ausencia...
Usualmente empleamos como medida de la contingencia un estadístico llamado delta-P, cuya formulita es algo así:
Delta-P = Probabilidad de A enpresencia de B - Probabilidad de A en ausencia de B.
Y, aterrizando por fin en nuestro tema, diré que la formulita también tiene traducción en términos de celdas en esa tabla que venía en el artículo. Veamos:
Cogemos el primer ejemplo que te he puesto. 48% de los muertos no llevaban cinurón, 52% de los muertos sí lo llevaba; 90% de los vivos sí lo llevaba, 10% de los vivos no. Lo traducimos a la tabla (tengo que dividir los porcentajes entre dos, simplemente porque la tabla representa todos los eventos, y por tanto deberían sumar 100%):
Celda a: 0,26 (52% entre 2). Los que mueren y llevan el cinto.
Celda b: 0,45 (90% entre 2). Los que no mueren y llevan el cinto.
Celda c: 0,24 (48% entre 2). Los que mueren y no llevan el cinto.
Celda d: 0,05 (10% entre 2). Los que no mueren y no llevan el cinto.
Ahora: Probabilidad de morir llevando el cinto = 0,26/(0,26+0,45) - 0,24/(0,24+0,05) = -0,46.
Espero haber planteado bien los cálculos y no haber metido la pata en los mismos.
La contingencia negativa que nos ha salido entre morir y llevar el cinto indica que ambos eventos covarían de manera sistemática, pero inversa, es decir, en cristiano: que cuando llevas el cinto es más probable que no mueras, y que si uno se ha muerto, es más probable que no llevara el cinto.
Prueba, si quieres, a aplicar la fórmula en otro de los supuestos y verás cómo la conclusión cambia drásticamente. Te ahorraré el trabajo: en el segundo ejemplo que te puse, la contingencia resultante es 0,49 (valor positivo). O sea, que es más probable morir si llevas el cinto, y si te has muerto, es más probable que llevaras el cinto. En el último ejemplo, la contingencia rsultante es cero: da igual que lleves el cinto o no, es irrelevante para tu supervivencia. Y todos esos resultados manteniendo constante la información que nos daba la noticia, sólo he ido proponiendo valores diferentes para la que no nos daba (la referida a los supervivientes).
Todo esto tiene su utilidad porque además darnos la mitad de la información así "a pelo" puede conducir a conclusiones aparentemente correctas pero muy equivocadas. Es lo que sucede con la llamada "tasa base": si todo el mundo se pone el cinturón de seguridad salvo unos pocos, es tremendamente probable que la mayoría de los muertos en accidente lo llevaran puesto. Eso no quiere decir que el cinturón no sirva, eso no lo podemos decir sin tener la otra parte de la información. Pero el hecho de que un porcentaje tan grande de los conductores lleven el cinturón lleva a la conclusión engañosa en la que tú mismo has caído. ¿Te das cuenta?
Bueno, menuda chapa te he soltado. Espero que no te hayas aburrido más de la cuenta. Un saludo.
Claro que si Kailho.
Y puesto que cada dia en el mundo mueren menos personas con cancer que personas sin cancer, es mejor tener cancer. Y puesto que mueren mas no-fumadores que fumadores es mejor fumar, y puesto que mueren mas de muerte natural que por suicidio, para vivir es mejor suicidarse.
Hablando de ignorancia matematica, espero que tu post fuera una broma.
ahora que me fijo el post de kailho es de febrero del 2006. Nada pues, es que llego a traves de malaprensa. agur
Best regards from NY!
keep posting like this it’s really very good idea, you are awesome!
paxil
Publicar un comentario