Razonamiento estadístico

En un tramo definido de una autopista, la posibilidad de que pase un coche en 30 minutos es de 0,95. ¿Cuál será la probabilidad de que pase un coche por el mismo tramo en 10 minutos?

Preguntas como esta, que parecen triviales y hasta un poco irritantes, ¡pueden suponer que consigas el trabajo de tu vida! Es que, recientemente, he tenido la oportunidad de leer algunas de las preguntas más curiosas que preparan los encargados de personal de la compañía Google para seleccionar a los candidatos a uno de sus jugosos puestos de trabajo. Aquí tenéis el enlace, no me voy a hacer de rogar, aunque aviso que está en inglés y que las preguntas son más difíciles de lo que parecen, a veces precisamente por ser realmente más sencillas de lo que uno piensa. El caso es que al leerlas y pensar en ellas (no diré cuántas he conseguido resolver) he recordado uno de esos temas intrigantes en la Psicología Cognitiva: el razonamiento estadístico. ¿Que no sabéis de qué hablo? Pues seguid leyendo.

Está bastante extendida (iba a decir "asumida") la propuesta de que las personas nos comportamos espontáneamente como “científicos intuitivos”, razonando para intentar averiguar cómo funciona el mundo. Aun a pesar de no disponer de los conocimientos necesarios para llevar ese razonamiento a buen puerto, realizamos el esfuerzo con todo el material disponible, de una manera intuitiva e informal, sin gran explicitación. Y a veces llegamos a conclusiones correctas. Pero a veces, también, no lo conseguimos y nos equivocamos.
Algún maligno pensará que los psicólogos disfrutamos exponiendo al público los errores y las limitaciones de nuestro sistema cognitivo. No hay más que echarle un vistazo a cualquier manual o libro de texto sobre Psicología del Pensamiento para sorprenderse con la cantidad de estudios que demuestran lo mal que se nos dan ciertos problemas de razonamiento lógico (aquí hablamos un día de la tarea de selección de Wason) o de otros tipos, al menos cuando los sujetos experimentales no han sido entrenados previamente en ese tipo de tareas. Digan lo que digan los malpensados, lo cierto es que los psicólogos no sacamos a la luz todas estas limitaciones del razonamiento humano (sólo) por maldad: estoy convencido de que los errores sistemáticos que cometen los seres humanos (me refiero a los errores sistemáticos y comunes) son muchísimo más informativos que cualquier ejecución perfecta en la misma tarea, de cara a obtener una idea de cuáles son los mecanismos implicados en el pensamiento. Pues bien, una vez hayáis excusado al bienintencionado investigador, diré que uno de los dominios donde las personas sin entrenamiento previo nos mostramos como auténticos patanes es el del razonamiento estadístico y probabilístico, el necesario para responder a la pregunta que inicia el post. Digamos que somos muy malos “estadísticos intuitivos”.

Los errores en las estimaciones estadísticas de las personas son variados y se han clasificado según el tipo de razonamiento estadístico implicado. Comenzaremos con cuestiones más sencillas que las que proponían en Google. Por ejemplo, se ha demostrado que nuestras estimaciones de la probabilidad de un suceso están muy influidas por el conocimiento a posteriori de si ese suceso en concreto ha tenido lugar. Introduzco una bola blanca en un bombo con nueve bolas negras. La probabilidad de que salga una bola blanca es una entre diez. Sin embargo, una vez que alguien nos informa de que se ha extraído una bola y que esa bola es blanca, tendemos a “ver muy claro” que la probabilidad de que saliese la bola blanca era mayor. Este “sesgo de a posteriori” recuerda a esos hinchas deportivos que están animadísimos con el rendimiento de su equipo favorito, pero que, una vez conocida la derrota en el último partido, manifiestan “haberla visto venir” desde hace tiempo. Todo el mundo “lo sabía” y a nadie pilla de sorpresa porque todo el mundo es muy listo. Resumiendo, que adivinar las cosas a toro pasado es muy fácil… y también engañoso.

Disponibilidad
Pero hay errores estadísticos generalizados y sistemáticos mucho más interesantes y menos obvios que el sesgo a posteriori. Kahneman y Tversky son dos autores que abordaron la cuestión y desarrollaron el uso del concepto “heurístico” para explicar este tipo de sesgos cognitivos. Lo que sucede, según estos señores, es que nuestros sistemas cognitivos basan la eficiencia en la capacidad de ahorrar, tanto en término de esfuerzos como en tiempo. Ante un problema relativamente complejo, que precisa para su resolución de una “inferencia” (un proceso de pensamiento lógico), el cerebro reacciona tomando un “atajo” (eso es, precisamente, el heurístico). Un camino más corto y rápido que, si bien no siempre conduce a la solución correcta, al menos proporciona una respuesta rápida y también razonable. Y es que, en la mayoría de las situaciones, es más importante obtener una respuesta inmediata, con tal de que no sea descabellada, que invertir un esfuerzo y tiempo desproporcionados para dar con la solución. En sus estudios, Tversky y Kahneman identifican distintas clases de heurísticos. El primero de ellos es el de la disponibilidad, que implica que a veces la probabilidad de un suceso se juzga en función de la facilidad con la que uno puede rememorar o imaginar ejemplos favorables a ese suceso. Es decir, que creeremos que un evento es más probable cuanto más disponible en la memoria esté un recuerdo o imaginación de que ese evento ha tenido lugar. El sesgo de a posteriori que comenté antes podría explicarse de esta manera: si acaba de salir del bombo una bola blanca, el suceso más fácilmente imaginable... es que salga del bombo una bola blanca.
Pero hay más ejemplos. Mucha gente confiesa su miedo a volar en avión, sobre todo después de haber tenido lugar algún accidente aéreo con gran repercusión mediática. Sin embargo, los accidentes de avión son estadísticamente raros, máxime al comprarlos con los muy frecuentes accidentes de circulación automovilística. El bombardeo mediático y las graves repercusiones de cada accidente aéreo (aun siendo éstos escasos) provocan que este tipo de sucesos estén muy disponibles en la memoria, magnificando la probabilidad que las personas les asignan.

Representatividad
En este vais a caer seguro. Igual que el heurístico de disponibilidad produce una preferencia por los sucesos fácilmente imaginables, el heurístico de representatividad fija una preferencia por los sucesos más representativos, estereotípicos, de su clase. Veamos cómo lo hacéis:

Linda tiene 31 años, es soltera, extrovertida y brillante. En sus tiempos de estudiante, estuvo comprometida con asuntos de discriminación y justicia social, y participó en numerosas manifestaciones. ¿Cuál de las siguientes afirmaciones sobre Linda es más probable?
1) Es cajera en un banco.
2) Es cajera en un banco y además una activista del movimiento feminista.

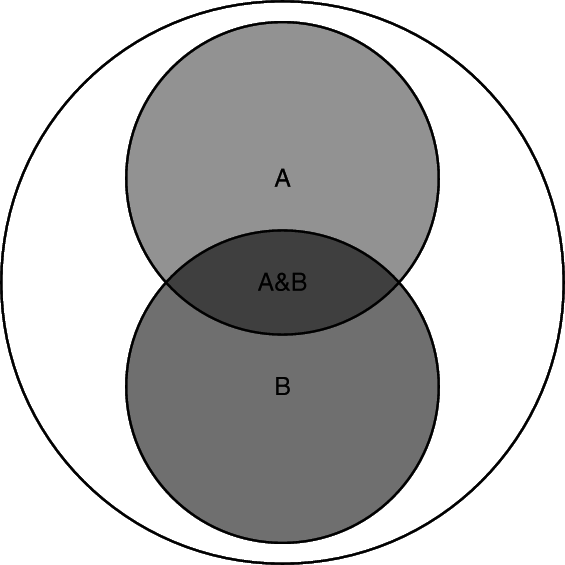
¿Cuántos habéis escogido la segunda opción? Fue la opción preferida por los participantes del estudio de Tversky y Kahneman de donde he extraído la pregunta. Pues, sabedlo ahora, ¡la segunda opción es falsa! Es fácil dejarse llevar y pasar por alto el hecho (comprobado) de que la probabilidad de que ocurra un suceso A siempre es mayor que la de que ocurra el mismo suceso A más un suceso adicional B. Se trata de una característica (necesaria) de la estructura lógica de las afirmaciones, no importa realmente el contenido de las mismas. Me gusta este tipo de problemas porque recuerda a uno de los principios básicos en la ciencia, el de la parsimonia. La hipótesis sencilla es casi siempre la más probable.
Lo que explica la preferencia por la opción equivocada es el poderoso atractivo de las respuestas representativas. Uno lee la descripción de Linda e inmediatamente advierte que encaja bien con el estereotipo de una activista del movimiento feminista (segunda opción). Linda es más representativa de las cajeras de banco feministas que de las cajeras de banco en general. Pero eso, como hemos visto, no debería afectar al razonamiento de probabilidad. En vez de razonar correctamente, tomamos el atajo del mecanismo heurístico que nos proporciona la respuesta rápida.

Este mismo heurístico de representatividad puede llevarnos a otros errores. Por ejemplo, leída la descripción de Linda, decidme: ¿Creéis más probable que sea militar, o bien que sea la presidenta de una asociación feminista de rango nacional? Responded sin trampas, ¿eh? Según los estudios de Tversky y Kahneman, predigo que muchos de vosotros escogeréis la segunda opción. De nuevo, Linda encaja como un guante en el estereotipo de una presidenta típica de una asociación feminista de rango nacional. Pero, ay, pasamos por alto un gran detalle, que es la “tasa base”. Hay muchos más militares que presidentas de una asociación feminista de rango nacional. Este dato debería al menos haberse incluido en nuestro razonamiento.

Tversky y Kahneman hablan también de un tercer heurístico, el de “anclaje y ajuste”, del que no voy a hablar esta vez. Creo que con lo expuesto hasta aquí es fácil hacerse una idea del tipo de limitaciones de nuestro sistema cognitivo a la hora de hacer frente a problemas de tipo estadístico. Soy consciente de que estoy sirviendo en bandeja una excusa perfecta para los estudiantes de secundaria a los que se les atragantan las matemáticas (con los cuales me identifico sinceramente). Aunque, por otro lado, los heurísticos nos ofrecen una explicación para muchos de estos errores sistemáticos sobre la premisa de que dichos errores son adaptativos. Como ya dije, es realmente útil contar con una respuesta rápida para el problema, aunque muchas veces no sea la solución correcta.

Por cierto, ya lo había olvidado. ¿Habéis dado con la solución al problema que abría el post? ¿Cuál será la probabilidad de que pase un coche en 10 minutos? Uhmmm.

Actualización (13-9-2007): Edito para añadir este enlace relacionado que nos manda Brainy del blog "El cerebro de Darwin", que no se ve bien en los comentarios y está interesante. Muchas gracias, compañero.